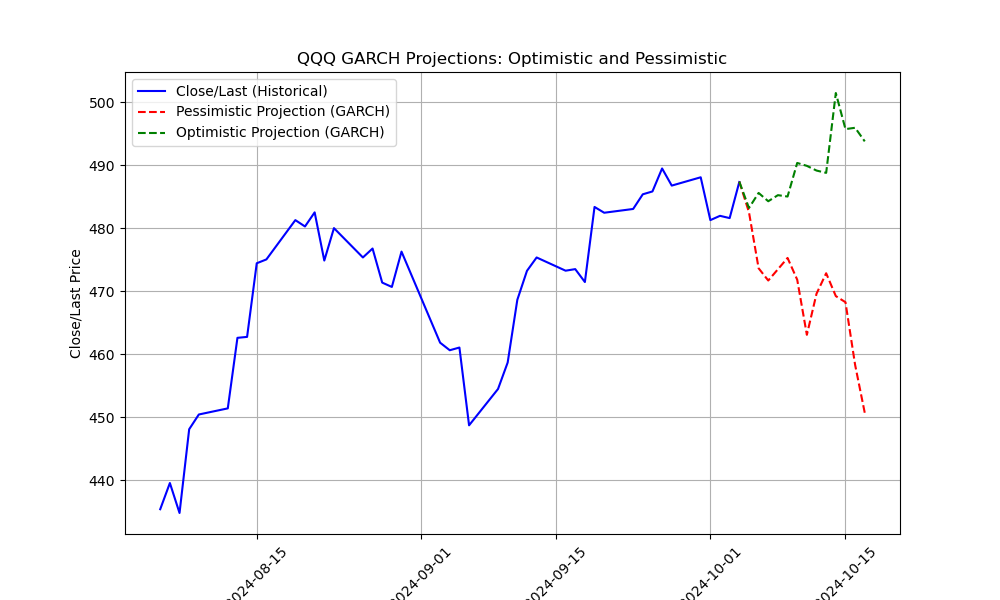
GARCH model applied to QQQ for week

Heteroskedasticity is a statistical concept that aims to describe when the variance of errors in a regression model is not constant across observations. What can it tell us about criticalities?

In order to build a solid set of sound projection functions, we need to apply a tried and tested method of examining data’s proclivity to exhibit what is often called “volatility clustering,” where, just like volatility compression, irregular spikes or flattened periods may signal entry and exit points into critical rupture events.

The Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model may be used to forecast volatility time series data¹. Furthermore, it may be of notable interest to consider any given time series data, test for heteroskedasticity and then proceed with forecasting if volatility clustering is identified.

For example, with Python using 5 year’s worth of QQQ data but focusing on the last year, we obtain the following result:

'Breusch-Pagan Test for Heteroskedasticity:\n==================================================\nLagrange multiplier statistic: 5.4968\np-value: 0.0191\nf-value: 5.5748\nf p-value: 0.0190\n\nConclusion: The p-value is less than 0.05, indicating that heteroskedasticity is present in the data. This suggests periods of increased volatility, potentially signaling the approach of critical rupture events in the stock market.\n'

Plotting the prices and projections results in the following:

The code used for this was:

import numpy as np
import pandas as pd
from statsmodels.api import add_constant, OLS
from statsmodels.stats.diagnostic import het_breuschpagan

# Redefine the file path and reload the CSV
file_path = 'QQQ.csv'

# Reload the CSV file and filter for the last two months
df = pd.read_csv(file_path)
df['Date'] = pd.to_datetime(df['Date'])
df = df.sort_values(by='Date')

# Filter the data for the last two months
last_two_months = df[df['Date'] >= (df['Date'].max() - pd.DateOffset(months=2))]

# Recompute the log returns for the last two months
log_returns = np.log(last_two_months['Close/Last']).diff().dropna()

# Set up the independent variable (constant and time index)
X = add_constant(log_returns.index.values)  # Constant and time index
y = log_returns  # Dependent variable: log returns

# Fit the regression model
model = OLS(y, X).fit()

# Perform the Breusch-Pagan test
bp_test = het_breuschpagan(model.resid, model.model.exog)

# Extract the test results
bp_test_labels = ['Lagrange multiplier statistic', 'p-value', 'f-value', 'f p-value']
bp_test_results = dict(zip(bp_test_labels, bp_test))

# Generate a verbose report
report = f"Breusch-Pagan Test for Heteroskedasticity:\n"
report += f"{'='*50}\n"
for label, result in bp_test_results.items():
    report += f"{label}: {result:.4f}\n"

# Explanation of heteroskedasticity presence
if bp_test_results['p-value'] < 0.05:
    report += "\nConclusion: The p-value is less than 0.05, indicating that heteroskedasticity is present in the data. This suggests periods of increased volatility, potentially signaling the approach of critical rupture events in the stock market.\n"
else:
    report += "\nConclusion: The p-value is greater than 0.05, indicating no significant heteroskedasticity. The data shows relatively stable volatility without critical rupture signals.\n"

print(report)

and for the chart:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from arch import arch_model

# Load the historical data and ensure the Date column is datetime formatted
historical_file = "QQQ.csv"   # Replace with the correct path to your historical data
historical_data = pd.read_csv(historical_file)
historical_data['Date'] = pd.to_datetime(historical_data['Date'])

# Function to load and process option chain data, skipping the first 3 rows
def load_option_chain(option_chain_file):
    # Load the CSV file, skipping the first 3 rows
    option_data = pd.read_csv(option_chain_file, skiprows=3)
    return option_data

# Load the option chain data
option_chain_file = "qqq_quotedata.csv"   # Replace with the correct path to your option chain data
option_data = load_option_chain(option_chain_file)

# Extract implied volatility from the option data for the analysis
implied_volatility = option_data['IV'].mean()

# Define the function to fit the GARCH model and project future prices with drift adjustment
def garch_projection(data, forecast_days=14, implied_vol=None, drift_adjustment=0):
    # Rescale the log returns
    returns = np.log(data['Close/Last']).diff().dropna() * 100  # Rescale by 100
    garch = arch_model(returns, vol='Garch', p=1, q=1)
    garch_fitted = garch.fit(disp="off")
    
    # Forecast volatility for the next 'forecast_days'
    garch_forecast = garch_fitted.forecast(horizon=forecast_days)
    forecast_volatility = garch_forecast.variance.values[-1, :]  # Extract forecast variance
    
    # Calculate drift (mean return over the historical data) and adjust by implied volatility and custom drift adjustment
    drift = returns.mean() + drift_adjustment
    if implied_vol is not None:
        drift += implied_vol  # Add implied volatility as a factor in the drift
    
    # Project future returns using the forecasted volatility and adjusted for drift
    last_price = data['Close/Last'].iloc[-1]  # Ensure last price is used properly
    projected_returns = np.random.normal(drift, np.sqrt(forecast_volatility), forecast_days)
    projected_prices = np.exp(np.cumsum(projected_returns) / 100) * last_price  # Ensure prices start at the last historical price
    
    # Generate future dates for the projection
    last_date = data['Date'].max()
    projected_dates = [last_date + pd.DateOffset(days=i) for i in range(1, forecast_days + 1)]
    
    return projected_dates, projected_prices, last_price, forecast_volatility

# Restrict the chart to the last two months of historical data
two_months_ago = historical_data['Date'].max() - pd.DateOffset(months=2)
last_two_months = historical_data[historical_data['Date'] >= two_months_ago]

# Perform GARCH projection for the next 2 weeks with implied volatility factored in
forecast_days = 14

# Pessimistic projection (negative drift adjustment)
# Pessimistic projection (negative drift adjustment)
pessimistic_dates, pessimistic_prices, last_price, pessimistic_volatility = garch_projection(
    last_two_months, forecast_days, implied_vol=implied_volatility, drift_adjustment=0.01)

# Optimistic projection (positive drift adjustment)
optimistic_dates, optimistic_prices, _, optimistic_volatility = garch_projection(
    last_two_months, forecast_days, implied_vol=implied_volatility, drift_adjustment=-0.01)

# Plot the historical data (last 2 months) and two GARCH projections
def plot_with_two_garch_projections(data, pessimistic_dates, pessimistic_prices, optimistic_dates, optimistic_prices, last_price):
    plt.figure(figsize=(10,6))
    
    # Plot historical data first (last 2 months)
    plt.plot(data['Date'], data['Close/Last'], label='Close/Last (Historical)', color='blue')
    
    # Manually apply vertical offset to both projections
    vertical_offset = last_price - pessimistic_prices[0] + 52
    pessimistic_prices = pessimistic_prices + vertical_offset
    
    vertical_offset = last_price - optimistic_prices[0] + 52
    optimistic_prices = optimistic_prices + vertical_offset
    
    # Adjust dates to match the price points
    pessimistic_dates = [data['Date'].max() + pd.DateOffset(days=i) for i in range(len(pessimistic_prices))]
    optimistic_dates = [data['Date'].max() + pd.DateOffset(days=i) for i in range(len(optimistic_prices))]

    # Plot pessimistic projection
    plt.plot(pessimistic_dates, pessimistic_prices, '--', label='Pessimistic Projection (GARCH)', color='red')

    # Plot optimistic projection
    plt.plot(optimistic_dates, optimistic_prices, '--', label='Optimistic Projection (GARCH)', color='green')

    # Labels and title
    plt.xlabel('Date')
    plt.ylabel('Close/Last Price')
    plt.title("QQQ GARCH Projections: Optimistic and Pessimistic")
    plt.legend()
    plt.grid(True)
    plt.xticks(rotation=45)
    plt.savefig("F:\\output\\garch\\QQQ_op.png")
    plt.show()

# Plot the optimistic and pessimistic GARCH projections
plot_with_two_garch_projections(last_two_months, pessimistic_dates, pessimistic_prices, optimistic_dates, optimistic_prices, last_price)

# Volatility analysis and critical rupture detection
def analyze_volatility(forecast_volatility, projected_dates):
    max_volatility_index = np.argmax(forecast_volatility)
    max_volatility_date = projected_dates[max_volatility_index]
    
    # Critical rupture estimated
    report = f"Anticipated Critical Rupture Event:\n"
    report += f"======================================\n"
    report += f"Highest forecasted volatility is expected on: {max_volatility_date.strftime('%Y-%m-%d')}\n"
    report += f"Estimated volatility on this date: {forecast_volatility[max_volatility_index]:.6f}\n"
    
    # Volatility compression analysis
    volatility_compression = np.min(forecast_volatility)
    min_volatility_index = np.argmin(forecast_volatility)
    compression_date = projected_dates[min_volatility_index]
    
    report += f"\nVolatility Compression Analysis:\n"
    report += f"Lowest forecasted volatility is expected on: {compression_date.strftime('%Y-%m-%d')}\n"
    report += f"Estimated minimum volatility: {volatility_compression:.6f}\n"
    
    return report

# Generate the volatility analysis report
volatility_report = analyze_volatility(forecast_volatility, projected_dates)
print(volatility_report)

1. https://www.investopedia.com/terms/h/heteroskedasticity.asp